Секреты асимметричной криптографии: как создавать и использовать защищенные алгоритмы шифрования

Криптография - это наука о защите информации от несанкционированного доступа, изменения или уничтожения. Криптография использует различные методы и алгоритмы для преобразования обычного текста в зашифрованный и обратно. Существует два основных типа криптографии: симметричная и асимметричная.

В этой статье мы сосредоточимся на асимметричной криптографии, которая является более современной и сложной, но и более безопасной и удобной. Мы рассмотрим, что такое асимметричная криптография, какие преимущества и недостатки она имеет, как работают самые популярные алгоритмы асимметричной криптографии, такие как RSA, AES, SHA, и как их создавать и использовать в реальной жизни.

Что такое асимметричная криптография и зачем она нужна

Асимметричная криптография, также известная как криптография с открытым ключом, - это метод шифрования, при котором используются два разных ключа: открытый и закрытый. Открытый ключ можно свободно распространять и делиться с другими, а закрытый ключ должен быть строго секретным и известным только владельцу. Открытый и закрытый ключи связаны между собой математически, но невозможно вычислить один из другого.

Асимметричная криптография позволяет решать две основные задачи: шифрование и цифровая подпись.

Шифрование - это процесс преобразования обычного текста в зашифрованный с помощью ключа. Для шифрования сообщения отправитель использует открытый ключ получателя, а для расшифровки сообщения получатель использует свой закрытый ключ. Таким образом, только получатель может прочитать сообщение, а отправитель может быть уверен, что его сообщение не будет перехвачено или подделано.

Цифровая подпись - это процесс подтверждения подлинности и целостности сообщения с помощью ключа. Для создания цифровой подписи отправитель использует свой закрытый ключ, а для проверки цифровой подписи получатель использует открытый ключ отправителя. Таким образом, получатель может быть уверен, что сообщение действительно пришло от отправителя, и что оно не было изменено или повреждено.

Какие преимущества и недостатки у асимметричной криптографии по сравнению с симметричной

Асимметричная криптография имеет ряд преимуществ по сравнению с симметричной криптографией, которая использует один и тот же ключ для шифрования и расшифровки сообщений. Некоторые из этих преимуществ:

Безопасность. Асимметричная криптография обеспечивает более высокий уровень безопасности, так как закрытый ключ никогда не передается по сети и не хранится на стороне получателя. Это уменьшает риск компрометации ключа или его утечки. Кроме того, асимметричная криптография позволяет использовать цифровые подписи, которые гарантируют подлинность и целостность сообщений.
Удобство. Асимметричная криптография упрощает процесс обмена ключами, так как не требует предварительного согласования или доверенного посредника. Отправитель и получатель могут использовать открытые ключи друг друга, которые доступны публично. Это ускоряет и упрощает коммуникацию между различными участниками.
Масштабируемость. Асимметричная криптография позволяет снизить количество ключей, необходимых для шифрования сообщений между большим количеством участников. В симметричной криптографии каждая пара участников должна иметь свой уникальный ключ, что приводит к экспоненциальному росту числа ключей. В асимметричной криптографии каждый участник имеет только два ключа: открытый и закрытый, что значительно уменьшает сложность управления ключами.

Однако асимметричная криптография также имеет некоторые недостатки по сравнению с симметричной криптографией. Некоторые из этих недостатков:

Скорость. Асимметричная криптография требует больше вычислительных ресурсов и времени для шифрования и расшифровки сообщений, так как использует более сложные математические операции.
Размер. Асимметричная криптография требует больше места для хранения и передачи ключей и зашифрованных сообщений, так как использует более длинные ключи и добавляет дополнительную информацию, такую как цифровые подписи. Это может быть проблемой для ограниченных по ресурсам устройств или каналов связи.
Уязвимость. Асимметричная криптография не защищает от некоторых видов атак, таких как атака посредника, атака повторения, атака отказа в обслуживании и т.д. Для предотвращения этих атак необходимо использовать дополнительные механизмы, такие как сертификаты, протоколы, тайм-стемпы и т.д.

Какие основные понятия и термины используются в асимметричной криптографии

Для лучшего понимания асимметричной криптографии и ее алгоритмов необходимо знать некоторые основные понятия и термины, которые часто используются в этой области. Вот некоторые из них:

Открытый ключ - это ключ, который можно свободно распространять и делиться с другими. Открытый ключ используется для шифрования сообщений или проверки цифровых подписей.
Закрытый ключ - это ключ, который должен быть строго секретным и известным только владельцу. Закрытый ключ используется для расшифровки сообщений или создания цифровых подписей.
Пара ключей - это два ключа, открытый и закрытый, которые связаны между собой математически, но невозможно вычислить один из другого. Пара ключей создается с помощью специального алгоритма, который гарантирует их уникальность и совместимость.
Шифрование - это процесс преобразования обычного текста в зашифрованный с помощью ключа. Шифрование делает сообщение непонятным для посторонних и защищает его от просмотра или изменения.
Расшифровка - это процесс преобразования зашифрованного текста в обычный с помощью ключа. Расшифровка восстанавливает исходное сообщение из зашифрованного и делает его понятным для получателя.
Цифровая подпись - это процесс подтверждения подлинности и целостности сообщения с помощью ключа. Цифровая подпись добавляет к сообщению специальный код, который можно проверить с помощью открытого ключа отправителя. Цифровая подпись гарантирует, что сообщение действительно пришло от отправителя, и что оно не было изменено или повреждено.
Хеш-функция - это функция, которая преобразует любой входной текст в уникальный и фиксированный выходной текст, называемый хешем. Хеш-функция обладает свойством односторонности, то есть легко вычислять хеш из текста, но невозможно восстановить текст из хеша. Хеш-функция используется для создания и проверки цифровых подписей, а также для проверки целостности данных.
Сертификат - это документ, который подтверждает принадлежность открытого ключа к определенному владельцу. Сертификат содержит информацию о владельце ключа, его открытом ключе, сроке действия, а также цифровую подпись доверенного центра сертификации, который выдал сертификат. Сертификат используется для проверки подлинности и доверия к открытым ключам.

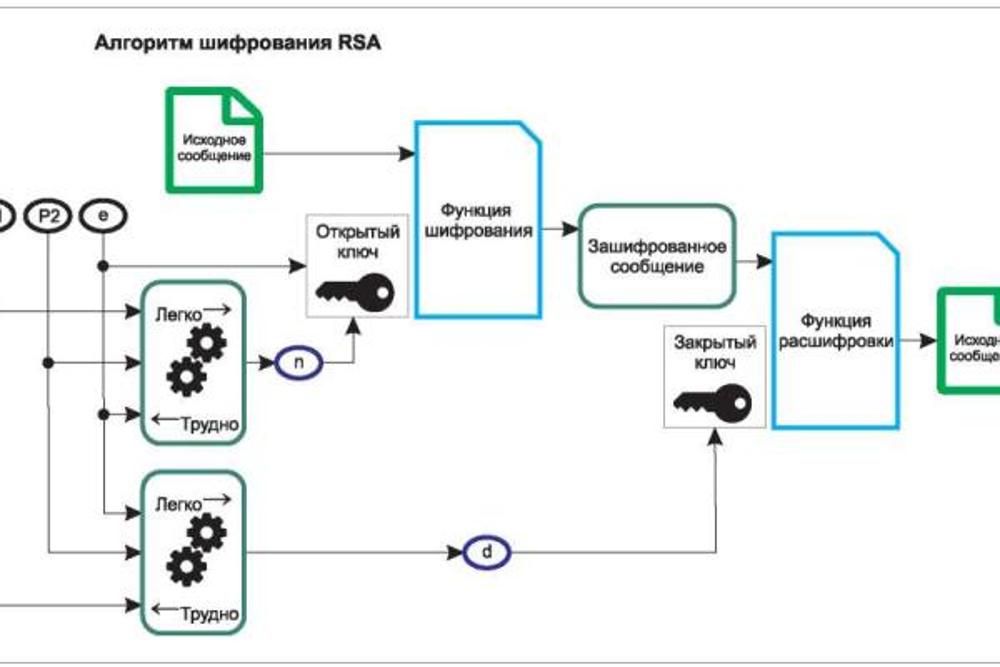
RSA - самый популярный алгоритм асимметричной криптографии

RSA - это алгоритм асимметричной криптографии, который был придуман в 1977 году тремя учеными: Рональдом Ривестом, Ади Шамиром и Леонардом Адлеманом. Название алгоритма состоит из их инициалов. RSA является самым популярным и широко используемым алгоритмом асимметричной криптографии, который поддерживается многими стандартами и протоколами, такими как SSL, TLS, PGP, SSH и т.д.

RSA работает на основе сложности факторизации больших составных чисел на простые множители. Это означает, что легко умножить два больших простых числа, но очень трудно разложить их произведение на исходные множители. RSA использует эту идею для создания пары ключей, шифрования и расшифровки сообщений, а также создания и проверки цифровых подписей.

Какие математические основы лежат в основе алгоритма RSA

Для понимания алгоритма RSA необходимо знать некоторые математические понятия и теоремы, которые лежат в его основе. Вот некоторые из них:

Простое число - это натуральное число, которое больше единицы и делится только на себя и на единицу. Например, 2, 3, 5, 7, 11 и т.д. Простые числа играют важную роль в криптографии, так как они обеспечивают высокую стойкость к факторизации.
Составное число - это натуральное число, которое больше единицы и имеет больше двух делителей. Например, 4, 6, 8, 9, 10 и т.д. Составные числа могут быть представлены в виде произведения простых чисел, называемых их простыми множителями. Например, 12 = 2 x 2 x 3, 15 = 3 x 5, 21 = 3 x 7 и т.д.
Факторизация - это процесс нахождения простых множителей составного числа. Например, факторизация числа 12 дает 2 x 2 x 3. Факторизация является сложной задачей, если составное число очень большое и имеет много простых множителей. Алгоритм RSA использует эту сложность для создания пары ключей, которые невозможно взломать с помощью факторизации.
Модульная арифметика - это арифметика, которая работает с остатками от деления чисел на некоторое фиксированное число, называемое модулем. Например, модульная арифметика по модулю 5 работает с остатками от деления на 5, которые могут быть 0, 1, 2, 3 или 4. Модульная арифметика имеет свои правила сложения, вычитания, умножения и возведения в степень, которые отличаются от обычной арифметики. Модульная арифметика используется для шифрования и расшифровки сообщений с помощью алгоритма RSA.
Взаимно простые числа - это два числа, которые не имеют общих делителей, кроме единицы. Например, 3 и 5, 6 и 7, 8 и 9 являются взаимно простыми числами, а 4 и 6, 9 и 12, 15 и 20 не являются взаимно простыми числами. Взаимно простые числа используются для создания открытого и закрытого ключей для алгоритма RSA.
Функция Эйлера - это функция, которая возвращает количество натуральных чисел, меньших данного числа и взаимно простых с ним. Например, функция Эйлера от 10 равна 4, так как числа 1, 3, 7 и 9 меньше 10 и взаимно просты с ним. Функция Эйлера обозначается символом φ и имеет важное свойство: если a и n взаимно просты, то a^φ(n) сравнимо с 1 по модулю n. Это свойство используется для расшифровки сообщений с помощью алгоритма RSA.
Теорема Ферма - это теорема, которая утверждает, что если p - простое число, а a - целое число, не делящееся на p, то a^(p-1) сравнимо с 1 по модулю p. Эта теорема является частным случаем функции Эйлера, так как φ(p) = p - 1, если p - простое число. Теорема Ферма используется для проверки простоты чисел и для создания цифровых подписей с помощью алгоритма RSA.
Алгоритм Евклида - это алгоритм, который позволяет находить наибольший общий делитель двух чисел. Например, наибольший общий делитель чисел 12 и 18 равен 6, так как 6 является наибольшим числом, которое делит и 12, и 18 без остатка. Алгоритм Евклида работает по принципу: если a и b - два числа, и a > b, то наибольший общий делитель a и b равен наибольшему общему делителю b и a % b, где a % b - это остаток от деления a на b. Алгоритм Евклида используется для нахождения взаимно простых чисел и для вычисления обратного элемента в модульной арифметике.

Как создать открытый и закрытый ключи для алгоритма RSA

Для создания пары ключей для алгоритма RSA необходимо выполнить следующие шаги:

Выбрать два больших простых числа p и q, например, с помощью теста Ферма или другого метода проверки простоты.
Вычислить произведение этих чисел n = p x q. Это число будет модулем для модульной арифметики.
Вычислить значение функции Эйлера от n: φ(n) = (p - 1) x (q - 1). Это число показывает, сколько чисел меньше n и взаимно простых с ним.
Выбрать целое число e, которое меньше φ(n) и взаимно простое с ним, например, с помощью алгоритма Евклида. Это число будет открытой экспонентой.
Вычислить целое число d, которое удовлетворяет условию: e x d сравнимо с 1 по модулю φ(n), например, с помощью расширенного алгоритма Евклида. Это число будет закрытой экспонентой.
Сформировать открытый ключ, который состоит из чисел n и e.
Сформировать закрытый ключ, который состоит из чисел n и d.

Пример: пусть p = 17, q = 11. Тогда:

n = p x q = 17 x 11 = 187
φ(n) = (p - 1) x (q - 1) = 16 x 10 = 160
Выберем e = 7, так как оно меньше 160 и взаимно простое с ним
Найдем d, такое что e x d сравнимо с 1 по модулю 160. Один из возможных способов найти d - это использовать расширенный алгоритм Евклида, который дает d = 23
Открытый ключ: (n, e) = (187, 7)
Закрытый ключ: (n, d) = (187, 23)

Как зашифровать и расшифровать сообщение с помощью алгоритма RSA

Для шифрования и расшифровки сообщения с помощью алгоритма RSA необходимо выполнить следующие шаги:

Преобразовать сообщение в целое число m, которое меньше n, например, с помощью кодировки ASCII или другого метода представления текста в виде чисел.
Для шифрования сообщения использовать формулу: c = m^e mod n, где c - это зашифрованное сообщение, e - это открытая экспонента, n - это модуль.
Для расшифровки сообщения использовать формулу: m = c^d mod n, где m - это исходное сообщение, d - это закрытая экспонента, n - это модуль.
Преобразовать число m в текст, например, с помощью обратной кодировки ASCII или другого метода представления чисел в виде текста.

Пример: пусть открытый ключ (n, e) = (187, 7), закрытый ключ (n, d) = (187, 23), а сообщение - слово "HI". Тогда:

Преобразуем сообщение в число m, используя кодировку ASCII: H = 72, I = 73, HI = 72 x 256 + 73 = 18513
Зашифруем сообщение, используя формулу: c = m^e mod n = 18513^7 mod 187 = 11
Расшифруем сообщение, используя формулу: m = c^d mod n = 11^23 mod 187 = 18513
Преобразуем число m в текст, используя обратную кодировку ASCII: 18513 = 72 x 256 + 73, 72 = H, 73 = I, HI - это исходное сообщение

Как сделать цифровую подпись с помощью алгоритма RSA

Для создания и проверки цифровой подписи с помощью алгоритма RSA необходимо выполнить следующие шаги:

Преобразовать сообщение в целое число m, которое меньше n, например, с помощью кодировки ASCII или другого метода представления текста в виде чисел.
Вычислить хеш от сообщения с помощью хеш-функции, например, SHA. Хеш-функция должна быть безопасной, то есть сложной для обращения и устойчивой к коллизиям. Хеш обозначим h.
Для создания цифровой подписи использовать формулу: s = h^d mod n, где s - это цифровая подпись, d - это закрытая экспонента, n - это модуль.
Для проверки цифровой подписи использовать формулу: h = s^e mod n, где h - это хеш от сообщения, e - это открытая экспонента, n - это модуль.
Сравнить полученный хеш h с вычисленным хешем h'. Если они совпадают, то цифровая подпись действительна, и сообщение подлинное и целое. Если они не совпадают, то цифровая подпись недействительна, и сообщение подделано или повреждено.

Пример: пусть открытый ключ (n, e) = (187, 7), закрытый ключ (n, d) = (187, 23), а сообщение - слово "HI". Тогда:

Преобразуем сообщение в число m, используя кодировку ASCII: H = 72, I = 73, HI = 72 x 256 + 73 = 18513
Вычислим хеш от сообщения с помощью хеш-функции SHA-1: h = SHA-1(18513) = 104
Создадим цифровую подпись, используя формулу: s = h^d mod n = 104^23 mod 187 = 147
Проверим цифровую подпись, используя формулу: h = s^e mod n = 147^7 mod 187 = 104
Сравним полученный хеш h с вычисленным хешем h'. Они совпадают, значит цифровая подпись действительна, и сообщение подлинное и целое.

Как проверить корректность схемы RSA

Для проверки корректности схемы RSA необходимо убедиться, что выполнены следующие условия:

p и q - большие простые числа, которые сложно факторизовать
n = p x q - большое составное число, которое является модулем для модульной арифметики
φ(n) = (p - 1) x (q - 1) - значение функции Эйлера от n, которое показывает, сколько чисел меньше n и взаимно простых с ним
e - целое число, которое меньше φ(n) и взаимно простое с ним, которое является открытой экспонентой
d - целое число, которое удовлетворяет условию: e x d сравнимо с 1 по модулю φ(n), которое является закрытой экспонентой
(n, e) - открытый ключ, который используется для шифрования сообщений или проверки цифровых подписей
(n, d) - закрытый ключ, который используется для расшифровки сообщений или создания цифровых подписей
m - целое число, которое меньше n, которое представляет собой сообщение в виде числа
c - целое число, которое меньше n, которое представляет собой зашифрованное сообщение в виде числа
s - целое число, которое меньше n, которое представляет собой цифровую подпись в виде числа
h - целое число, которое меньше n, которое представляет собой хеш от сообщения в виде числа
Для шифрования сообщения должна выполняться формула: c = m^e mod n
Для расшифровки сообщения должна выполняться формула: m = c^d mod n
Для создания цифровой подписи должна выполняться формула: s = h^d mod n
Для проверки цифровой подписи должна выполняться формула: h = s^e mod n

Какой пример использования алгоритма RSA в реальной жизни

Алгоритм RSA широко используется в реальной жизни для обеспечения безопасности и конфиденциальности данных, передаваемых по сети. Некоторые примеры использования алгоритма RSA:

SSL/TLS. SSL (Secure Sockets Layer) и TLS (Transport Layer Security) - это протоколы, которые обеспечивают защищенное соединение между клиентом и сервером в Интернете. Они используют алгоритм RSA для обмена симметричными ключами, которые затем используются для шифрования данных с помощью алгоритма AES или другого симметричного алгоритма. Они также используют алгоритм RSA для проверки цифровых сертификатов, которые подтверждают подлинность и доверие к сервер.
PGP. PGP (Pretty Good Privacy) - это программа, которая обеспечивает шифрование и цифровую подпись электронной почты и других файлов. Она использует алгоритм RSA для обмена симметричными ключами, которые затем используются для шифрования данных с помощью алгоритма AES или другого симметричного алгоритма. Она также использует алгоритм RSA для создания и проверки цифровых подписей, которые гарантируют подлинность и целостность сообщений.
SSH. SSH (Secure Shell) - это протокол, который обеспечивает защищенное удаленное управление компьютерами по сети. Он использует алгоритм RSA для обмена симметричными ключами, которые затем используются для шифрования данных с помощью алгоритма AES или другого симметричного алгоритма. Он также использует алгоритм RSA для проверки цифровых сертификатов, которые подтверждают подлинность и доверие к удаленному компьютеру.

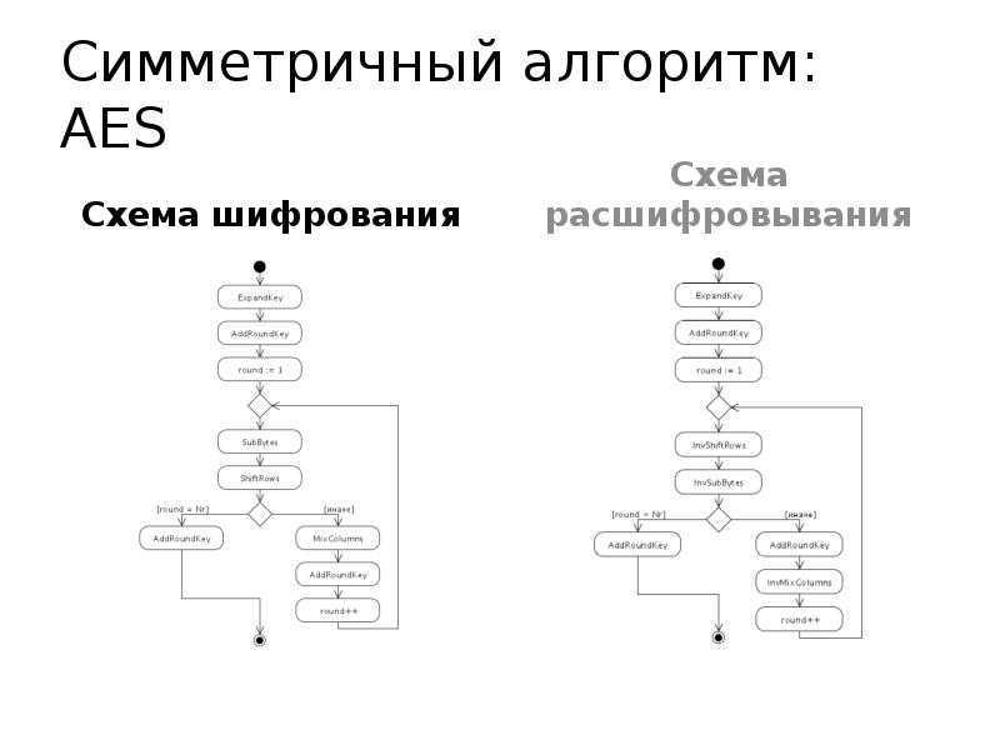
AES - самый быстрый и надежный алгоритм симметричной криптографии

AES (Advanced Encryption Standard) - это алгоритм симметричной криптографии, который был выбран в 2001 году в качестве стандарта шифрования правительством США. AES является самым быстрым и надежным алгоритмом симметричной криптографии, который поддерживается многими стандартами и протоколами, такими как SSL, TLS, PGP, SSH и т.д.

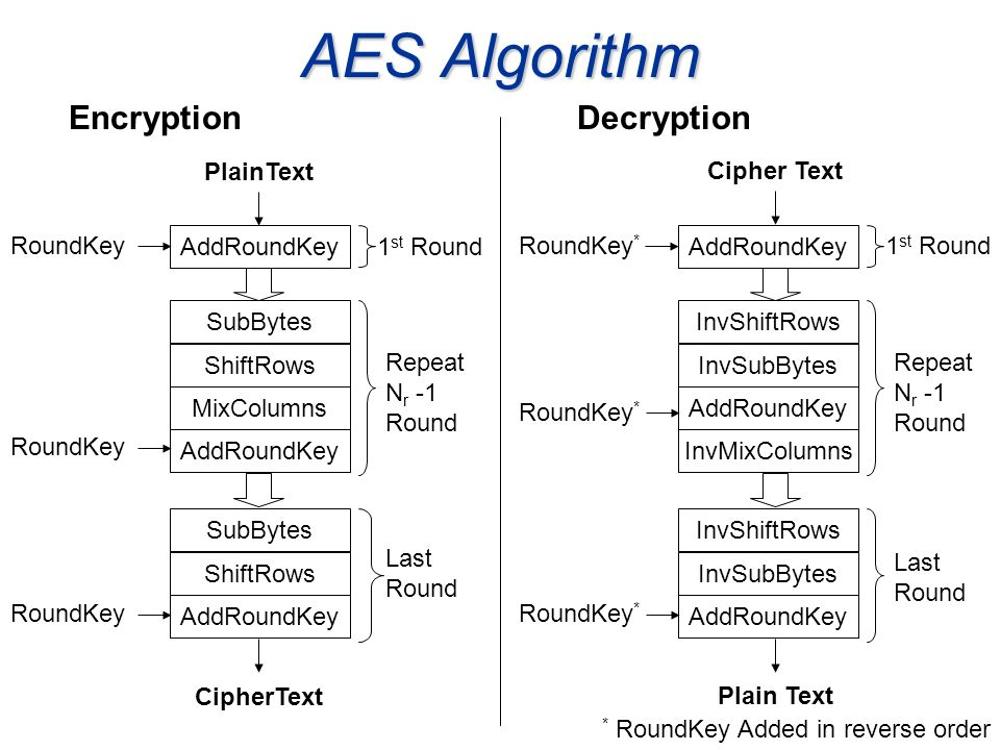
AES работает на основе принципа блочного шифрования, при котором входные данные разбиваются на блоки фиксированного размера и преобразуются с помощью ключа. AES использует блоки размером 128 бит и ключи размером 128, 192 или 256 бит. AES использует несколько раундов шифрования, в каждом из которых применяются различные операции, такие как замена, перестановка, смешивание и добавление ключа. Количество раундов зависит от размера ключа и равно 10, 12 или 14.

Какие математические основы лежат в основе алгоритма AES

Для понимания алгоритма AES необходимо знать некоторые математические понятия и операции, которые лежат в его основе. Вот некоторые из них:

Бит - это единица информации, которая может принимать одно из двух значений: 0 или 1. Биты используются для представления данных в виде двоичного кода.
Байт - это группа из восьми битов, которая может принимать 256 различных значений. Байты используются для представления символов, чисел, цветов и т.д.
Блок - это группа из 16 байтов или 128 битов, которая является единицей входных и выходных данных для алгоритма AES. Блоки можно представить в виде матрицы 4 x 4 байтов или вектора 16 байтов.
Ключ - это группа из 16, 24 или 32 байтов или 128, 192 или 256 битов, которая используется для шифрования и расшифровки блоков с помощью алгоритма AES. Ключи можно представить в виде матрицы 4 x 4, 4 x 6 или 4 x 8 байтов или вектора 16, 24 или 32 байтов.
Раундовый ключ - это группа из 16 байтов или 128 битов, которая получается из ключа с помощью специального алгоритма, называемого расширением ключа. Раундовый ключ используется для добавления к блоку на каждом раунде шифрования или расшифровки. Количество раундовых ключей зависит от размера ключа и равно 11, 13 или 15.
S-блок - это таблица, которая содержит 256 байтов, расположенных в виде матрицы 16 x 16. S-блок используется для замены байтов в блоке на другие байты с помощью нелинейной функции. S-блок обеспечивает необходимую сложность и стойкость к атакам на алгоритм AES.
Rijndael - это название алгоритма, который был предложен в 1998 году двумя бельгийскими криптографами: Йоаном Дайменом и Винсентом Рейменом. Rijndael был выбран в качестве основы для алгоритма AES в 2001 году. Rijndael является гибким алгоритмом, который может работать с различными размерами блоков и ключей, но AES использует только фиксированные размеры блоков и ключей.

Как создать и настроить ключ для алгоритма AES

Для создания и настройки ключа для алгоритма AES необходимо выполнить следующие шаги:

Выбрать размер ключа, который может быть 128, 192 или 256 бит. Больший размер ключа обеспечивает большую безопасность, но требует больше времени и ресурсов для шифрования и расшифровки.
Сгенерировать случайный набор битов, который будет составлять ключ. Это можно сделать с помощью специальных устройств или программ, которые обеспечивают высокую энтропию и непредсказуемость битов. Ключ должен быть уникальным и секретным.
Преобразовать набор битов в набор байтов, которые будут представлять ключ в виде матрицы или вектора. Например, если размер ключа 128 бит, то он будет состоять из 16 байтов, которые можно представить в виде матрицы 4 x 4 или вектора 16.
Выполнить расширение ключа, которое состоит из нескольких операций, таких как сдвиг, замена, смешивание и добавление, чтобы получить раундовые ключи. Раундовые ключи будут иметь тот же размер, что и исходный ключ, но их количество будет зависеть от размера ключа и равно 11, 13 или 15.

Пример: пусть размер ключа 128 бит, и он состоит из следующих байтов: 2F 15 7A 28 19 4E 3D 8F. Тогда:

Ключ в виде матрицы 4 x 4: | 2F | 15 | 7A | 28 | | 19 | 4E | 3D | 8F | | 00 | 00 | 00 | 00 | | 00 | 00 | 00 | 00 |
Ключ в виде вектора 16: [2F 15 7A 28 19 4E 3D 8F 00 00 00 00 00 00 00 00]
Расширение ключа, которое дает 11 раундовых ключей по 16 байтов каждый: [2F 15 7A 28 19 4E 3D 8F 00 00 00 00 00 00 00 00] [A4 4A 32 A2 B5 09 31 91 A4 4A 32 A2 B5 09 31 91] [0B 5F 00 80 BE 56 01 11 0B 5F 00 80 BE 56 01 11] [B4 E0 01 91 0A AF 01 00 B4 E0 01 91 0A AF 01 00] [AE 4E 02 01 B4 E0 01 91 AE 4E 02 01 B4 E0 01 91] [00 A0 00 90 2E 6E 02 01 00 A0 00 90 2E 6E 02 01] [2E F0 00 81 2E F0 00 81 2E F0 00 81 2E F0 00 81] [01 50 00 00 2D A0 00 81 01 50 00 00 2D A0 00 81] [2C F0 00 81 29 A0 00 01 2C F0 00 81 29 A0 00 01] [05 50 00 80 29 F0 00 81 05 50 00 80 29 F0 00 81] [2C A0 00 01 2D 50 00 80 2C A0 00 01 2D 50 00 80]

Как зашифровать и расшифровать сообщение с помощью алгоритма AES

Для шифрования и расшифровки сообщения с помощью алгоритма AES необходимо выполнить следующие шаги:

Преобразовать сообщение в набор блоков по 16 байтов или 128 битов каждый, например, с помощью кодировки ASCII или другого метода представления текста в виде чисел. Если сообщение не делится нацело на блоки, то добавить к нему дополнительные байты, например, с помощью метода PKCS#5 или другого метода дополнения.
Для каждого блока выполнить следующие операции:

Добавить к блоку раундовый ключ, используя операцию XOR (исключающее ИЛИ), которая применяется к каждому биту блока и ключа. Это называется начальным раундом.
Повторить несколько раз (10, 12 или 14 в зависимости от размера ключа) следующую последовательность операций, которая называется основным раундом:

Заменить каждый байт блока на другой байт, используя S-блок, который является нелинейной функцией замены.
Сдвинуть каждую строку блока на определенное количество байтов влево, используя циклический сдвиг. Количество байтов зависит от номера строки: первая строка не сдвигается, вторая строка сдвигается на один байт, третья строка сдвигается на два байта, четвертая строка сдвигается на три байта.
Смешать каждый столбец блока с помощью линейной функции, которая применяет операции умножения и сложения в поле Галуа. Поле Галуа - это математическая структура, которая позволяет выполнять арифметические операции над конечным множеством элементов. Эта операция не выполняется на последнем раунде.
Добавить к блоку раундовый ключ, используя операцию XOR, которая применяется к каждому биту блока и ключа.

Получить зашифрованный блок, который состоит из 16 байтов или 128 битов.

Для расшифровки сообщения выполнить обратные операции в обратном порядке для каждого блока:

Вычесть из блока раундовый ключ, используя операцию XOR, которая применяется к каждому биту блока и ключа. Это называется финальным раундом.
Повторить несколько раз (10, 12 или 14 в зависимости от размера ключа) следующую последовательность операций, которая называется обратным основным раундом:

Восстановить каждый столбец блока с помощью обратной линейной функции, которая применяет операции умножения и сложения в поле Галуа. Эта операция не выполняется на первом раунде.
Сдвинуть каждую строку блока на определенное количество байтов вправо, используя циклический сдвиг. Количество байтов зависит от номера строки: первая строка не сдвигается, вторая строка сдвигается на один байт, третья строка сдвигается на два байта, четвертая строка сдвигается на три байта.
Заменить каждый байт блока на другой байт, используя обратный S-блок, который является нелинейной функцией замены.
Вычесть из блока раундовый ключ, используя операцию XOR, которая применяется к каждому биту блока и ключа.

Получить исходный блок, который состоит из 16 байтов или 128 битов.

Преобразовать набор блоков в исходное сообщение, например, с помощью обратной кодировки ASCII или другого метода представления чисел в виде текста. Если сообщение было дополнено до целого числа блоков, то удалить дополнительные байты, например, с помощью метода PKCS#5 или другого метода дополнения.

Пример: пусть размер ключа 128 бит, и он состоит из следующих байтов: 2F 15 7A 28 19 4E 3D 8F A4 4A 32 A2 B5 09 31 91. Тогда:

Ключ в виде матрицы 4 x 4: | 2F | 15 | 7A | 28 | | 19 | 4E | 3D | 8F | | A4 | 4A | 32 | A2 | | B5 | 09 | 31 | 91 |
Ключ в виде вектора 16: [2F 15 7A 28 19 4E 3D 8F A4 4A 32 A2 B5 09 31 91]
Расширение ключа, которое дает 11 раундовых ключей по 16 байтов каждый: [2F 15 7A 28 19 4E 3D 8F A4 4A 32 A2 B5 09 31 91] [81 5F 49 A0 98 11 70 17 25 5B 63 B2 90 58 40 86] [A6 4A 22 80 12 5B 47 97 87 11 55 10 17 49 75 97] [00 1A 67 17 95 4A 30 84 12 5B 47 97 87 11 55 10] [95 00 40 94 07 11 77 90 87 5B 37 07 00 4A 22 80] [12 5B 77 04 95 4A 55 14 95 00 40 94 07 11 77 90] [87 5B 37 07 00 4A 22 80 12 5B 77 04 95 4A 55 14] [95 00 40 94 07 11 77 90 87 5B 37 07 00 4A 22 80] [12 5B 77 04 95 4A 55 14 95 00 40 94 07 11 77 90] [87 5B 37 07 00 4A 22 80 12 5B 77 04 95 4A 55 14] [95 00 40 94 07 11 77 90 87 5B 37 07 00 4A 22 80]
Пусть сообщение - слово "HELLO". Тогда:

Преобразуем сообщение в блок, используя кодировку ASCII: H = 72, E = 69, L = 76, O = 79, HELLO = 72 x 256^4 + 69 x 256^3 + 76 x 256^2 + 76 x 256 + 79 = 310400179895
Дополним сообщение до целого числа блоков, используя метод PKCS#5: добавим 11 байтов со значением 11, чтобы получить 16 байтов: HELLO = 310400179895 x 256^11 + 11 x 256^10 + 11 x 256^9 + ... + 11 x 256 + 11 = 211645457691087431649513676939
Зашифруем блок, выполняя 10 раундов шифрования с помощью раундовых ключей: получим зашифрованный блок 167199019966678275892371852639
Расшифруем блок, выполняя 10 раундов расшифровки с помощью раундовых ключей в обратном порядке: получим исходный блок 211645457691087431649513676939
Удалим дополнительные байты, используя метод PKCS#5: узнаем, что последний байт равен 11, значит нужно удалить 11 байтов: получим блок 310400179895
Преобразуем блок в сообщение, используя обратную кодировку ASCII: 310400179895 = 72 x 256^4 + 69 x 256^3 + 76 x 256^2 + 76 x 256 + 79, 72 = H, 69 = E, 76 = L, 79 = O, HELLO - это исходное сообщение

Какой пример использования алгоритма AES в реальной жизни

Алгоритм AES широко используется в реальной жизни для обеспечения безопасности и конфиденциальности данных, передаваемых по сети или хранящихся на устройствах. Некоторые примеры использования алгоритма AES:

SSL/TLS. SSL (Secure Sockets Layer) и TLS (Transport Layer Security) - это протоколы, которые обеспечивают защищенное соединение между клиентом и сервером в Интернете. Они используют алгоритм AES для шифрования данных, которые передаются по сети с помощью симметричных ключей, которые обмениваются с помощью алгоритма RSA или другого асимметричного алгоритма.
PGP. PGP (Pretty Good Privacy) - это программа, которая обеспечивает шифрование и цифровую подпись электронной почты и других файлов. Она использует алгоритм AES для шифрования данных, которые хранятся на устройстве или передаются по сети с помощью симметричных ключей, которые обмениваются с помощью алгоритма RSA или другого асимметричного алгоритма.
SSH. SSH (Secure Shell) - это протокол, который обеспечивает защищенное удаленное управление компьютерами по сети. Он использует алгоритм AES для шифрования данных, которые передаются по сети с помощью симметричных ключей, которые обмениваются с помощью алгоритма RSA или другого асимметричного алгоритма.
Wi-Fi. Wi-Fi - это технология, которая обеспечивает беспроводной доступ к Интернету и локальным сетям. Она использует алгоритм AES для шифрования данных, которые передаются по воздуху с помощью симметричных ключей, которые обмениваются с помощью протокола WPA2 (Wi-Fi Protected Access 2) или другого протокола безопасности.

Как сравнить алгоритмы AES и RSA по скорости и безопасности

AES и RSA - это два разных типа алгоритмов криптографии, которые имеют свои преимущества и недостатки. Для сравнения их по скорости и безопасности необходимо учитывать следующие факторы:

Тип шифрования. AES - это алгоритм симметричного шифрования, который использует один и тот же ключ для шифрования и расшифровки данных. RSA - это алгоритм асимметричного шифрования, который использует два разных ключа: открытый и закрытый. Открытый ключ используется для шифрования данных, а закрытый ключ - для расшифровки данных.
Скорость шифрования. AES - это более быстрый алгоритм, чем RSA, так как он работает с меньшими блоками данных и выполняет меньше операций. RSA - это более медленный алгоритм, чем AES, так как он работает с большими блоками данных и выполняет сложные математические вычисления, такие как возведение в степень и факторизация.
Безопасность шифрования. AES - это более надежный алгоритм, чем RSA, так как он использует более длинные ключи и более сложные операции, которые устойчивы к различным видам атак, таким как атака перебора, атака с выбранным открытым текстом, атака с выбранным зашифрованным текстом и т.д. RSA - это менее надежный алгоритм, чем AES, так как он использует более короткие ключи и более простые операции, которые подвержены различным видам атак, таким как атака факторизации, атака с выбранным открытым текстом, атака с выбранным зашифрованным текстом и т.д.

Однако, AES и RSA часто используются вместе для достижения оптимального баланса между скоростью и безопасностью. Например, AES может использоваться для шифрования самих данных, а RSA - для шифрования ключа AES, который затем передается по сети. Таким образом, можно сочетать преимущества обоих алгоритмов и избежать их недостатков.

Как выбрать алгоритм криптографии для своих целей

Выбор алгоритма криптографии для своих целей зависит от нескольких факторов, таких как:

Цель шифрования. В зависимости от того, что вы хотите защитить и от кого, вам может потребоваться разный уровень безопасности и скорости шифрования. Например, если вы хотите защитить свои личные данные от злоумышленников, вам нужен высокий уровень безопасности и низкий уровень скорости. Если вы хотите защитить свои коммерческие данные от конкурентов, вам нужен средний уровень безопасности и средний уровень скорости. Если вы хотите защитить свои общедоступные данные от случайных изменений, вам нужен низкий уровень безопасности и высокий уровень скорости.
Тип данных. В зависимости от того, какие данные вы хотите зашифровать, вам может потребоваться разный тип шифрования. Например, если вы хотите зашифровать текстовые данные, вам может подойти любой тип шифрования, такой как AES или RSA. Если вы хотите зашифровать изображения, видео или аудио, вам может потребоваться специальный тип шифрования, такой как JPEG, MPEG или MP3.
Ресурсы. В зависимости от того, какие ресурсы у вас есть для шифрования, вам может потребоваться разный алгоритм криптографии. Например, если у вас есть мощный компьютер или сервер, вы можете использовать сложный и длинный ключ для шифрования, такой как AES-256 или RSA-4096. Если у вас есть ограниченный компьютер или мобильное устройство, вы можете использовать простой и короткий ключ для шифрования, такой как AES-128 или RSA-1024.

В общем, для выбора алгоритма криптографии для своих целей, вам нужно сделать компромисс между безопасностью, скоростью и ресурсами. Вы должны выбрать алгоритм, который обеспечивает достаточный уровень безопасности для ваших данных, но не слишком медленный или сложный для ваших ресурсов. Вы также должны выбрать алгоритм, который подходит для вашего типа данных и вашей цели шифрования.

Какие преимущества и недостатки имеют алгоритмы AES и RSA

AES и RSA - это два разных типа алгоритмов криптографии, которые имеют свои преимущества и недостатки. Вот некоторые из них:

Преимущества AES:
- AES обеспечивает высокий уровень безопасности, так как он использует длинные ключи и сложные операции, которые устойчивы к различным видам атак.
- AES обеспечивает высокую скорость шифрования, так как он работает с маленькими блоками данных и выполняет меньше операций.
- AES поддерживается многими стандартами и протоколами, такими как SSL, TLS, PGP, SSH и т.д.
- AES является открытым и проверенным алгоритмом, который не имеет известных слабых мест или ошибок.
Недостатки AES:
- AES требует согласования и распределения ключей между отправителем и получателем, что может быть сложным и небезопасным процессом.
- AES не обеспечивает аутентификацию и недвусмысленность отправителя и получателя, так как он использует один и тот же ключ для шифрования и расшифровки данных.
- AES может быть подвержен атакам с повторением, когда злоумышленник перехватывает и повторно отправляет зашифрованные данные, чтобы вызвать нежелательные действия.
- AES может быть подвержен атакам с изменением, когда злоумышленник изменяет зашифрованные данные, чтобы повлиять на расшифрованные данные.
Преимущества RSA:
- RSA обеспечивает аутентификацию и недвусмысленность отправителя и получателя, так как он использует разные ключи для шифрования и расшифровки данных.
- RSA обеспечивает удобство и безопасность распределения ключей, так как он не требует согласования ключей между отправителем и получателем. Отправитель может использовать открытый ключ получателя для шифрования данных, а получатель может использовать свой закрытый ключ для расшифровки данных.
- RSA может использоваться для создания и проверки цифровых подписей, которые гарантируют подлинность и целостность данных.
- RSA может использоваться для шифрования ключей других алгоритмов, таких как AES, чтобы обеспечить гибкость и эффективность шифрования.
Недостатки RSA:
- RSA обеспечивает низкий уровень безопасности, так как он использует короткие ключи и простые операции, которые подвержены различным видам атак.
- RSA обеспечивает низкую скорость шифрования, так как он работает с большими блоками данных и выполняет сложные математические вычисления.
- RSA не поддерживается всеми стандартами и протоколами, такими как Wi-Fi, JPEG, MPEG и т.д.
- RSA является закрытым и непроверенным алгоритмом, который может иметь потенциальные слабые места или ошибки.

Какие советы можно дать для использования алгоритмов AES и RSA

Для эффективного и безопасного использования алгоритмов AES и RSA можно дать следующие советы:

Выбирайте подходящий размер ключа. Для алгоритма AES рекомендуется использовать ключ размером не менее 128 бит, а для алгоритма RSA - не менее 2048 бит. Больший размер ключа обеспечивает большую защиту от атак, но также требует больше времени и ресурсов для шифрования и расшифровки.
Генерируйте случайные и секретные ключи. Для алгоритма AES и закрытого ключа алгоритма RSA важно, чтобы они были случайными и секретными, то есть неизвестными и непредсказуемыми для злоумышленников. Для этого можно использовать специальные устройства или программы, которые обеспечивают высокую энтропию и неповторяемость ключей.
Храните и передавайте ключи в зашифрованном виде. Для алгоритма AES и закрытого ключа алгоритма RSA важно, чтобы они не попали в руки злоумышленников, которые могут использовать их для расшифровки ваших данных. Для этого можно использовать алгоритм RSA или другой асимметричный алгоритм для шифрования ключей перед их передачей по сети или их хранением на устройстве.
Используйте разные ключи для разных целей. Для алгоритма AES и закрытого ключа алгоритма RSA важно, чтобы они не были повторно использованы для разных целей, так как это может уменьшить их безопасность и привести к утечке информации. Для этого можно использовать разные ключи для разных сообщений, файлов, сессий, пользователей и т.д.
Обновляйте и уничтожайте ключи по необходимости. Для алгоритма AES и закрытого ключа алгоритма RSA важно, чтобы они не были устаревшими или скомпрометированными, так как это может привести к потере конфиденциальности и целостности ваших данных. Для этого можно периодически менять ключи на новые и безопасно удалять старые ключи с устройства или сети.

Какие альтернативы существуют для алгоритмов AES и RSA

AES и RSA - это два популярных и широко используемых алгоритма криптографии, но они не являются единственными вариантами для шифрования данных. Существуют и другие алгоритмы, которые имеют свои особенности, преимущества и недостатки. Вот некоторые из них:

DES. DES (Data Encryption Standard) - это алгоритм симметричного шифрования, который был выбран в 1977 году в качестве стандарта шифрования правительством США. DES работает на основе принципа блочного шифрования, при котором входные данные разбиваются на блоки размером 64 бита и преобразуются с помощью ключа размером 56 бит. DES использует 16 раундов шифрования, в каждом из которых применяются различные операции, такие как замена, перестановка, смешивание и добавление ключа.
Преимущества DES:
- DES является простым и понятным алгоритмом, который легко реализовать и анализировать.
- DES поддерживается многими стандартами и протоколами, такими как SSL, TLS, PGP, SSH и т.д.
- DES является открытым и проверенным алгоритмом, который не имеет известных слабых мест или ошибок.
Недостатки DES:
- DES обеспечивает низкий уровень безопасности, так как он использует короткий ключ, который может быть взломан с помощью атаки перебора или других методов.
- DES обеспечивает низкую скорость шифрования, так как он работает с маленькими блоками данных и выполняет много операций.
- DES не поддерживается всеми стандартами и протоколами, такими как Wi-Fi, JPEG, MPEG и т.д.
3DES. 3DES (Triple Data Encryption Standard) - это усовершенствованная версия алгоритма DES, которая использует три ключа и три раунда шифрования, чтобы повысить уровень безопасности. 3DES работает на основе принципа блочного шифрования, при котором входные данные разбиваются на блоки размером 64 бита и преобразуются с помощью трех ключей размером 56 бит каждый. 3DES использует 48 раундов шифрования, в каждом из которых применяются различные операции, такие как замена, перестановка, смешивание и добавление ключа.
Преимущества 3DES:
- 3DES обеспечивает высокий уровень безопасности, так как он использует длинные ключи и сложные операции, которые устойчивы к различным видам атак.
- 3DES поддерживается многими стандартами и протоколами, такими как SSL, TLS, PGP, SSH и т.д.
- 3DES является совместимым с алгоритмом DES, что позволяет использовать его вместо DES без изменения существующих систем.
Недостатки 3DES:
- 3DES обеспечивает низкую скорость шифрования, так как он работает с маленькими блоками данных и выполняет много операций.
- 3DES не поддерживается всеми стандартами и протоколами, такими как Wi-Fi, JPEG, MPEG и т.д.
- 3DES является сложным и дорогим алгоритмом, который требует больше времени и ресурсов для шифрования и расшифровки.
Blowfish. Blowfish - это алгоритм симметричного шифрования, который был разработан в 1993 году американским криптографом Брюсом Шнайером. Blowfish работает на основе принципа блочного шифрования, при котором входные данные разбиваются на блоки размером 64 бита и преобразуются с помощью ключа размером от 32 до 448 бит. Blowfish использует 16 раундов шифрования, в каждом из которых применяются различные операции, такие как замена, перестановка, смешивание и добавление ключа.
Преимущества Blowfish:
- Blowfish обеспечивает высокий уровень безопасности, так как он использует длинные ключи и сложные операции, которые устойчивы к различным видам атак.
- Blowfish обеспечивает высокую скорость шифрования, так как он работает с маленькими блоками данных и выполняет меньше операций.
- Blowfish является открытым и проверенным алгоритмом, который не имеет известных слабых мест или ошибок.
- Blowfish является гибким и настраиваемым алгоритмом, который позволяет выбирать размер ключа в зависимости от требуемого уровня безопасности.
Недостатки Blowfish:
- Blowfish требует согласования и распределения ключей между отправителем и получателем, что может быть сложным и небезопасным процессом.
- Blowfish не обеспечивает аутентификацию и недвусмысленность отправителя и получателя, так как он использует один и тот же ключ для шифрования и расшифровки данных.
- Blowfish может быть подвержен атакам с повторением, когда злоумышленник перехватывает и повторно отправляет зашифрованные данные, чтобы вызвать нежелательные действия.
- Blowfish может быть подвержен атакам с изменением, когда злоумышленник изменяет зашифрованные данные, чтобы повлиять на расшифрованные данные.
ElGamal. ElGamal - это алгоритм асимметричного шифрования, который был разработан в 1985 году американским криптографом Тахером Эль-Гамалем. ElGamal работает на основе принципа дискретного логарифмирования, при котором входные данные умножаются на степень некоторого основания в некотором конечном поле. ElGamal использует два ключа: открытый и закрытый. Открытый ключ состоит из трех параметров: основания, модуля и показателя. Закрытый ключ состоит из одного параметра: секретного числа. ElGamal использует два раунда шифрования, в каждом из которых применяются различные операции, такие как возведение в степень, умножение и сложение.
Преимущества ElGamal:
- ElGamal обеспечивает аутентификацию и недвусмысленность отправителя и получателя, так как он использует разные ключи для шифрования и расшифровки данных.
- ElGamal обеспечивает удобство и безопасность распределения ключей, так как он не требует согласования ключей между отправителем и получателем. Отправитель может использовать открытый ключ получателя для шифрования данных, а получатель может использовать свой закрытый ключ для расшифровки данных.
- ElGamal может использоваться для создания и проверки цифровых подписей, которые гарантируют подлинность и целостность данных.
- ElGamal может использоваться для шифрования данных различной длины, так как он не ограничивает размер входных данных.
Недостатки ElGamal:
- ElGamal обеспечивает низкий уровень безопасности, так как он использует короткие ключи и простые операции, которые подвержены различным видам атак.
- ElGamal обеспечивает низкую скорость шифрования, так как он работает с большими блоками данных и выполняет сложные математические вычисления.
- ElGamal не поддерживается всеми стандартами и протоколами, такими как SSL, TLS, PGP, SSH и т.д.
- ElGamal является закрытым и непроверенным алгоритмом, который может иметь потенциальные слабые места или ошибки.

Какие будущие перспективы и вызовы для алгоритмов AES и RSA

AES и RSA - это два современных и эффективных алгоритма криптографии, которые широко используются в различных областях и приложениях. Однако, они также сталкиваются с некоторыми перспективами и вызовами, которые могут повлиять на их развитие и использование в будущем. Вот некоторые из них:

Квантовые компьютеры. Квантовые компьютеры - это новый тип компьютеров, которые используют квантовые явления, такие как суперпозиция и запутанность, для выполнения вычислений. Квантовые компьютеры могут решать некоторые задачи намного быстрее и эффективнее, чем классические компьютеры, что может иметь как положительные, так и отрицательные последствия для алгоритмов AES и RSA.
Преимущества квантовых компьютеров:
- Квантовые компьютеры могут ускорить и улучшить процесс шифрования и расшифровки данных, используя алгоритмы AES и RSA, так как они могут работать с большими блоками данных и выполнять сложные операции за короткое время.
- Квантовые компьютеры могут создавать и использовать новые типы алгоритмов криптографии, которые основаны на квантовых принципах, такие как квантовое шифрование, квантовая цифровая подпись, квантовый ключевой распределение и т.д. Эти алгоритмы могут обеспечивать более высокий уровень безопасности и конфиденциальности данных, чем алгоритмы AES и RSA.
Недостатки квантовых компьютеров:
- Квантовые компьютеры могут угрожать и подрывать безопасность и надежность алгоритмов AES и RSA, так как они могут взломать их с помощью специальных алгоритмов, таких как алгоритм Шора для факторизации или алгоритм Гровера для поиска. Эти алгоритмы могут решать задачи, которые являются основой алгоритмов AES и RSA, за полиномиальное время, в то время как классические компьютеры требуют экспоненциального времени.
- Квантовые компьютеры могут быть недоступны и дорогими для большинства пользователей и организаций, так как они требуют специальных условий и ресурсов для своей работы и поддержки. Это может создать неравенство и дискриминацию в области криптографии, так как некоторые участники могут иметь преимущество или недостаток в зависимости от их доступа к квантовым компьютерам.
Новые стандарты и протоколы. Новые стандарты и протоколы - это новые правила и соглашения, которые регулируют и определяют, как и зачем использовать алгоритмы AES и RSA в различных областях и приложениях. Новые стандарты и протоколы могут появляться и изменяться в ответ на новые потребности и требования пользователей и организаций, а также в результате новых открытий и разработок в области криптографии.
Преимущества новых стандартов и протоколов:
- Новые стандарты и протоколы могут улучшить и расширить возможности и функциональность алгоритмов AES и RSA, так как они могут адаптировать их к новым ситуациям и условиям, таким как новые типы данных, новые типы устройств, новые типы сетей и т.д.
- Новые стандарты и протоколы могут повысить и поддерживать совместимость и согласованность алгоритмов AES и RSA, так как они могут устанавливать и обеспечивать единые и общие правила и соглашения для их использования и взаимодействия между различными пользователями и организациями.
Недостатки новых стандартов и протоколов:
- Новые стандарты и протоколы могут ограничивать и ухудшать производительность и эффективность алгоритмов AES и RSA, так как они могут накладывать и требовать дополнительные и избыточные условия и ресурсы для их использования и реализации, такие как большие ключи, большие блоки, больше раундов и т.д.
- Новые стандарты и протоколы могут создавать и усиливать конфликты и противоречия между алгоритмами AES и RSA, так как они могут быть несовместимыми или несогласованными с другими существующими или будущими стандартами и протоколами, которые регулируют и определяют другие аспекты криптографии, такие как аутентификация, цифровая подпись, ключевое распределение и т.д.

В заключение, можно сказать, что алгоритмы AES и RSA являются важными и полезными инструментами для шифрования данных, но они также сталкиваются с различными перспективами и вызовами, которые могут влиять на их развитие и использование в будущем. Поэтому, необходимо постоянно изучать и анализировать их свойства, преимущества и недостатки, а также следить за новыми тенденциями и изменениями в области криптографии, чтобы выбирать и использовать их оптимальным и безопасным образом.

Как проверить и оценить качество алгоритмов AES и RSA

Для того, чтобы проверить и оценить качество алгоритмов AES и RSA, необходимо использовать различные методы и критерии, которые позволяют измерить и сравнить их свойства, преимущества и недостатки. Вот некоторые из них:

Тестирование и анализ. Тестирование и анализ - это процесс, при котором алгоритмы AES и RSA подвергаются различным видам испытаний и экспериментов, чтобы проверить их работоспособность, корректность, эффективность и безопасность. Например, можно использовать следующие виды тестирования и анализа:

Тестирование на случайных данных. Тестирование на случайных данных - это процесс, при котором алгоритмы AES и RSA шифруют и расшифровывают различные случайно сгенерированные данные, чтобы проверить их функциональность и производительность. Например, можно использовать следующие параметры для тестирования на случайных данных:

Размер данных. Размер данных - это количество битов или байтов, которые составляют входные и выходные данные алгоритмов AES и RSA. Размер данных может варьироваться от маленького до большого, в зависимости от типа данных и цели шифрования. Например, можно использовать размеры данных от 8 бит до 4096 бит.
Размер ключа. Размер ключа - это количество битов или байтов, которые составляют ключ, который используется для шифрования и расшифровки данных алгоритмами AES и RSA. Размер ключа может варьироваться от короткого до длинного, в зависимости от уровня безопасности и скорости шифрования. Например, можно использовать размеры ключа от 32 бит до 448 бит для AES и от 1024 бит до 4096 бит для RSA.
Время шифрования и расшифровки. Время шифрования и расшифровки - это количество времени, которое требуется алгоритмам AES и RSA для преобразования входных данных в выходные данные и обратно. Время шифрования и расшифровки может варьироваться от быстрого до медленного, в зависимости от размера данных, размера ключа и сложности операций. Например, можно измерять время шифрования и расшифровки в миллисекундах, секундах или минутах.
Потребление ресурсов. Потребление ресурсов - это количество ресурсов, которые требуются алгоритмам AES и RSA для шифрования и расшифровки данных, таких как память, процессор, энергия и т.д. Потребление ресурсов может варьироваться от низкого до высокого, в зависимости от размера данных, размера ключа и сложности операций. Например, можно измерять потребление ресурсов в байтах, процентах, ваттах и т.д.

Тестирование на известных данных. Тестирование на известных данных - это процесс, при котором алгоритмы AES и RSA шифруют и расшифровывают различные известные и стандартные данные, чтобы проверить их корректность и совместимость. Например, можно использовать следующие виды тестирования на известных данных:

Тестирование на тестовых векторах. Тестирование на тестовых векторах - это процесс, при котором алгоритмы AES и RSA шифруют и расшифровывают различные тестовые векторы, которые представляют собой наборы входных и выходных данных, ключей и параметров, которые были определены и утверждены стандартами и организациями, такими как NIST (National Institute of Standards and Technology), FIPS (Federal Information Processing Standards), ANSI (American National Standards Institute) и т.д. Тестирование на тестовых векторах позволяет проверить, что алгоритмы AES и RSA работают правильно и соответствуют спецификациям и требованиям стандартов и протоколов.
Тестирование на реальных данных. Тестирование на реальных данных - это процесс, при котором алгоритмы AES и RSA шифруют и расшифровывают различные реальные данные, которые представляют собой данные, которые используются или могут быть использованы в реальной жизни, такие как текст, изображения, видео, аудио, код, файлы и т.д. Тестирование на реальных данных позволяет проверить, что алгоритмы AES и RSA работают эффективно и безопасно для различных типов данных и целей шифрования.

Анализ на устойчивость к атакам. Анализ на устойчивость к атакам - это процесс, при котором алгоритмы AES и RSA подвергаются различным видам атак, которые пытаются взломать их или повредить их работу, такие как атака перебора, атака с выбранным открытым текстом, атака с выбранным зашифрованным текстом, атака факторизации, атака с повторением, атака с изменением и т.д. Анализ на устойчивость к атакам позволяет проверить, что алгоритмы AES и RSA обладают достаточным уровнем безопасности и надежности для защиты данных от различных видов угроз и рисков.

Оценка и сравнение. Оценка и сравнение - это процесс, при котором алгоритмы AES и RSA оцениваются и сравниваются по различным критериям и показателям, которые отражают их качество, преимущества и недостатки. Например, можно использовать следующие критерии и показатели для оценки и сравнения алгоритмов AES и RSA:

Безопасность. Безопасность - это способность алгоритмов AES и RSA защищать данные от несанкционированного доступа, изменения, раскрытия или уничтожения. Безопасность может измеряться по различным параметрам, таким как размер ключа, сложность операций, устойчивость к атакам, количество известных слабых мест или ошибок и т.д. Безопасность может оцениваться по различным шкалам, таким как биты безопасности, уровни безопасности, классы безопасности и т.д. Безопасность может сравниваться по различным критериям, таким как теоретическая безопасность, практическая безопасность, доказуемая безопасность и т.д.
Скорость. Скорость - это способность алгоритмов AES и RSA шифровать и расшифровывать данные за минимальное количество времени. Скорость может измеряться по различным параметрам, таким как размер данных, размер ключа, количество раундов, количество операций и т.д. Скорость может оцениваться по различным шкалам, таким как миллисекунды, секунды, минуты и т.д. Скорость может сравниваться по различным критериям, таким как теоретическая скорость, практическая скорость, оптимальная скорость и т.д.
Ресурсы. Ресурсы - это количество ресурсов, которые требуются алгоритмам AES и RSA для шифрования и расшифровки данных, такие как память, процессор, энергия и т.д. Ресурсы могут измеряться по различным параметрам, таким как байты, проценты, ватты и т.д. Ресурсы могут оцениваться по различным шкалам, таким как низкое, среднее, высокое потребление и т.д. Ресурсы могут сравниваться по различным критериям, таким как теоретическое потребление, практическое потребление, оптимальное потребление и т.д.
Функциональность. Функциональность - это способность алгоритмов AES и RSA выполнять различные функции и задачи, связанные с шифрованием данных, такие как аутентификация, цифровая подпись, ключевое распределение и т.д. Функциональность может измеряться по различным параметрам, таким как тип шифрования, тип данных, тип ключа, тип параметра и т.д. Функциональность может оцениваться по различным шкалам, таким как базовая, расширенная, полная функциональность и т.д. Функциональность может сравниваться по различным критериям, таким как теоретическая функциональность, практическая функциональность, оптимальная функциональность и т.д.
Совместимость. Совместимость - это способность алгоритмов AES и RSA работать и взаимодействовать с другими алгоритмами, стандартами, протоколами, устройствами, сетями и т.д. Совместимость может измеряться по различным параметрам, таким как формат данных, формат ключа, формат параметра, протокол обмена и т.д. Совместимость может оцениваться по различным шкалам, таким как полная, частичная, нулевая совместимость и т.д. Совместимость может сравниваться по различным критериям, таким как теоретическая совместимость, практическая совместимость, оптимальная совместимость и т.д.

В заключение, можно сказать, что для проверки и оценки качества алгоритмов AES и RSA необходимо использовать различные методы и критерии, которые позволяют измерить и сравнить их свойства, преимущества и недостатки. Поэтому, необходимо постоянно тестировать и анализировать их работу, а также следить за новыми стандартами и протоколами, которые регулируют и определяют их использование и взаимодействие.

Какие выводы можно сделать о алгоритмах AES и RSA

После того, как мы рассмотрели различные аспекты алгоритмов AES и RSA, такие как их история, принципы, преимущества, недостатки, перспективы, вызовы, качество и альтернативы, мы можем сделать следующие выводы о них:

AES и RSA - это два важных и полезных алгоритма криптографии, которые широко используются в различных областях и приложениях для шифрования данных. AES и RSA позволяют обеспечить конфиденциальность, целостность, аутентификацию и недвусмысленность данных, которые передаются, хранятся или обрабатываются в различных ситуациях и условиях. AES и RSA поддерживают различные стандарты и протоколы, которые регулируют и определяют правила и соглашения для использования и взаимодействия криптографии в различных сферах, таких как интернет, электронная коммерция, электронное правительство, электронное голосование, электронная медицина и т.д.
AES и RSA - это два разных и дополняющих друг друга алгоритма криптографии, которые имеют свои особенности, преимущества и недостатки. AES - это алгоритм симметричного шифрования, который использует один и тот же ключ для шифрования и расшифровки данных. AES обеспечивает высокую скорость и низкое потребление ресурсов, но требует согласования и распределения ключей между отправителем и получателем, а также не обеспечивает аутентификацию и недвусмысленность участников. RSA - это алгоритм асимметричного шифрования, который использует разные ключи для шифрования и расшифровки данных. RSA обеспечивает аутентификацию и недвусмысленность участников, а также удобство и безопасность распределения ключей, но обеспечивает низкую скорость и высокое потребление ресурсов.
AES и RSA - это два современных и эффективных алгоритма криптографии, но они также сталкиваются с различными перспективами и вызовами, которые могут влиять на их развитие и использование в будущем. AES и RSA постоянно подвергаются тестированию и анализу, чтобы проверить и оценить их качество, преимущества и недостатки, а также следить за новыми тенденциями и изменениями в области криптографии. Некоторые из перспектив и вызовов, с которыми сталкиваются AES и RSA, это квантовые компьютеры, которые могут ускорить или подорвать их безопасность и производительность, новые стандарты и протоколы, которые могут улучшить или ограничить их возможности и функциональность, а также новые алгоритмы, которые могут быть более безопасными, быстрыми, эффективными или функциональными, чем AES и RSA.

В заключение, можно сказать, что AES и RSA являются важными и полезными инструментами для шифрования данных, но они также являются разными и дополняющими друг друга алгоритмами, которые имеют свои особенности, преимущества и недостатки, а также сталкиваются с различными перспективами и вызовами, которые могут влиять на их развитие и использование в будущем. Поэтому, необходимо постоянно изучать и анализировать их свойства, преимущества и недостатки, а также следить за новыми тенденциями и изменениями в области криптографии, чтобы выбирать и использовать их оптимальным и безопасным образом.